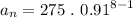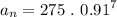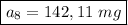Question

(100) points!!!! Help please

Georgie took 275 mg of medicine for her cold in the first hour she got home from work. In each
subsequent hour, the amount of medicine in her body is 91% of the amount from the previous
hour.
What is the explicit rule for the amount of medicine remaining in her body in the nth hour and
approximately how much medicine would remain in the 8th hour?
Round to two decimal places.
Drag and drop the answers into the boxes to match the situation.

Answer 1

`\displaystyle a_8=142,11\ mg`

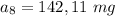
Explanation:

Geometric sequence

Each term in a geometric sequence can be computed as the previous term by a constant number called the common ratio. The formula to get the term n is

`\displaystyle a_n=a_1r^(n-1)`

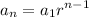
where
`a_1` is the first term of the sequence

The problem describes Georgie took 275 mg of the medicine for her cold in the first hour and that in each subsequent hour, the amount of medicine in her body is 91% (0.91) of the amount from the previous hour. It can be written as

amount in hour n = amount in hour n-1 * 0.91

a)

This information provides the necessary data to write the general term as

`\displaystyle a_n=275\ .\ 0.91^(n-1)`

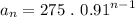
b)

In the 8th hour (n=8), the remaining medicine present is Georgie's body is

`\displaystyle a_n=275\ .\ 0.91^(8-1)`

`\displaystyle a_n=275\ .\ 0.91^(7)`

`\boxed{\displaystyle a_8=142,11\ mg}`