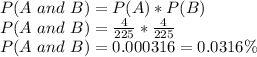Answer:
a) Independent
b) P(A and B) = 0.000316 or 0.0316%
Explanation:
a) Since it is specified that the selection of the coin in event B happens with replacement, the events are independent because each event does not interfere in the probability of the other. If there was no replacement, whether a rare coin was selected or not in event A would impact event B and then event B would depend on A.
b) For each event, there is a 4 in 225 chance of selecting a rare Indian penny. Therefore, P (A and B) is: