Question

A careful photographic survey of Jupiter's moon Io by the spacecraft Voyager 1 showed active volcanoes spewing liquid sulfur to heights of 70 km above the surface of this moon. If the value of g on Io is 2.0 m/s2 , estimate the speed with which the liquid sulfur left the volcano.

Answer 1

The concept used to solve this problem is that given in the kinematic equations of motion. From theory we know that the change in velocities of a body is equivalent to twice the distance traveled by acceleration, in other words:

`v_f^2-v_i^2 = 2ax`

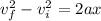
Where,

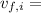`v_(f,i) =` Final and initial velocity

a = Acceleration

x = Displacement

For the given case, the displacement is equivalent to the height (x = h) and the acceleration is the same gravitational acceleration (a = g). In turn we do not have initial speed therefore

`v_f^2 = 2hg`

`v_f = √(2hg)`

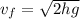
Our values are given as

`h = 70km = 70*10^3m`

`g = 2m/s^2`

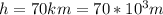
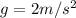
Replacing we have that,

`v_f = √(2hg)`

`v_f = √(2(70*10^3)(2))`

`v_f = 529.15m/s`

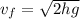
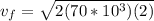
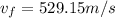
Therefore the speed with which the liquid sulfur left the volcano is 529.15m/s