Question

Consider the following distribution of objects: a 5.00-kg object with its center of gravity at (0, 0) m, a 3.00-kg object at (0, 4.00) m, and a 4.00-kg object at (3.00, 0) m. Where should a fourth object of mass 8.00 kg be placed so that the center of gravity of the four-object arrangement will be at (0, 0)?

Answer 1

(-1.5,-1.5)m

Step-by-step explanation:

we know that:

`X_(cm) = (m_1x_1+m_2x_2....m_nX_n)/(m_1+m_2...m_n)`

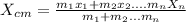
where
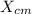`X_(cm)` is the location of the center of gravity in the axis x,
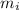`m_i` is the mass of the object i and
`x_i` the first coordinate of center of gravity of object i.

so:

`0 = ((5kg)(0)+(3kg)(0)+(4kg)(3)+(8kg)x_4)/(5kg+3kg+4kg+8kg)`

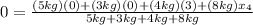
Where
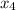`x_4` is the first coordinate of the center of gravity for the fourth object.

Therefore, solving for
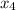`x_4`, we get:

`x_4 = -1.5m`

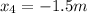
At the same way:

`Y_(cm) = (m_1y_1+m_2y_2....m_ny_n)/(m_1+m_2...m_n)`

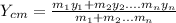
where
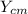`Y_(cm)` is the location of the center of gravity in the axis y,
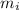`m_i` is the mass of the object i and
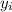`y_i` the second coordinate of center of gravity of object i. replacing values we get:

`Y_(cm) = ((5kg)(0)+(3kg)(4)+(4kg)(0)+(8kg)y_4)/(5+3+4+8)`

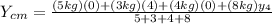
Where
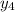`y_4` is the second coordinate of the center of gravity for the fourth object.

solving for
`y_4`:

`y_4 = -1.5m`

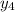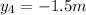
It means that the object of mass 8kg have to be placed in the

coordinates (-1.5,-1.5) m.