Question

3. A block of mass m1=1.5 kg on an inclined plane of an angle of 12° is connected by a cord over a mass-less, frictionless pulley to a second block of a mass m2= 1.2 kg hanging vertically. If the hanging block falls 0.92m

in 1.23 s, what is the coefficient of friction between m1 and the inclined plane?

Please show work

Answer 1

`\mu=0.377`

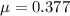
Step-by-step explanation:

we need to start by drawing the free body diagram for each of the masses in the system. Please see attached image for reference.

We have identified in green the forces on the blocks due to acceleration of gravity (
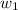`w_1` and
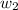`w_2`) which equal the product of the block's mass times "g".

On the second block (
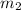`m_2`), there are just two forces acting: the block's weight (
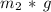`m_2\,*\,g`) and the tension (T) of the string. We know that this block is being accelerated since it has fallen 0.92 m in 1.23 seconds. We can find its acceleration with this information, and then use it to find the value of the string's tension (T). We would need both these values to set the systems of equations for block 1 in order to find the requested coefficient of friction.

To find the acceleration of block 2 (which by the way is the same acceleration that block 1 has since the string doesn't stretch) we use kinematics of an accelerated object, making use of the info on distance it fell (0.92 m) in the given time (1.23 s):

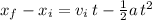`x_f-x_i=v_i\,t-(1)/(2) a\,t^2` and assume there was no initial velocity imparted to the block:

`x_f-x_i=v_i\,t-(1)/(2) a\,t^2\\-0.92\,m=0\,-(1)/(2) a\,(1.23)^2\\a=(0.92\,*\,2)/(1.23^2) \\a=1.216 \,(m)/(s^2)`

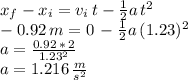
Now we use Newton's second law in block 2, stating that the net force in the block equals the block's mass times its acceleration:

`F_(net)=m_2\,a\\w_2-T=m_2\,a\\m_2\,g-T=m_2\,a\\m_2\,g-m_2\,a=T\\m_2\,(g-a)=T\\1.2\,(9.8-1.216)\,N=T\\T=10.3008\,N`

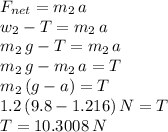
We can round this tension (T) value to 10.3 N to make our calculations easier.

Now, with the info obtained with block 2 (a - 1.216
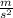`(m)/(s^2)`, and T = 10.3 N), we can set Newton's second law equations for block 1.

To make our study easier, we study forces in a coordinate system with the x-axis parallel to the inclined plane, and the y-axis perpendicular to it. This way, the motion in the y axis is driven by the y-component of mass' 1 weight (weight1 times cos(12) -represented with a thin grey trace in the image) and the normal force (n picture in blue in the image) exerted by the plane on the block. We know there is no acceleration or movement of the block in this direction (the normal and the x-component of the weight cancel each other out), so we can determine the value of the normal force (n):

`n-m_1\,g\,cos(12^o)=0\\n=m_1\,g\,cos(12^o)\\n=1.5\,*\,9.8\,cos(12^o)\\n=14.38\,N`

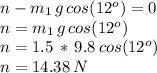
Now we can set the more complex Newton's second law for the net force acting on the x-axis for this block. Pointing towards the pulley (direction of the resultant acceleration
`a`), we have the string's tension (T). Pointing in the opposite direction we have two forces: the force of friction (f ) with the plane, and the x-axis component of the block's weight (weight1 times sin(12)):

`F_(net)=m_1\,a\\T-f-w_1\,sin(12)=m_1\,a\\T-w_1\,sin(12)-m_1\,a=f\\f=[10.3-1.5\,*\,9.8\,sin(12)-1.5\,*1.216]\,N\\f=5.42\,N`

And now, we recall that the force of friction equals the product of the coefficient of friction (our unknown
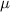`\mu`) times the magnitude of the normal force (14.38 N):

`f=\mu\,n\\5.42\,N=\mu\,*\,14.38\,N\\\mu=(5.42)/(14.38)\\\mu=0.377`

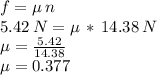
with no units.