Question

In Pennsylvania, the average IQ score is 101.5. The variable is normally distributed and the population standard deviation is 15. A school superintendent claims that the students in her school district have an IQ higher than the average of 101.5. She selects a random sample of 30 students and finds the mean of the test scores is 106.4.

Test the claim at α = 0.05

1. State the hypotheses and identify the claim.H0:μ=101.5H1:μ>101.5This is the claim, and this indicates a right-tailed test
2. Find the critical value. For a right-tailed test with α = 0.05, the z-value is +1.65.
3. Compute the test statistic.

Answer 1

Answer with explanation:

Let
`\mu` denotes the population mean.

1. Claim : The students in her school district have an IQ higher than the average of 101.5.

As per given , we have

Null hypothesis :
`H_0: \mu=101.5`

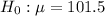
Alternative hypothesis:
`H_1: \mu>101.5`

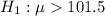
∵Alternative hypothesis is right-tailed , this indicates a right-tailed test

Also, Population standard deviation =
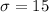`\sigma=15` , we use z-test.

sample size = 30

sample mean =
`\overline{x}=106.4`

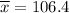
2. According to the z-table , the critical z-value for the right-tailed test with α = 0.05 is +1.65.

i.e. Critical value = 1.65

3. Test statistic :
`z=\frac{\overline{x}-\mu}{(\sigma)/(√(n))}`

`\\\\=(106.4-101.5)/((15)/(√(30)))\\\\=(4.9)/((15)/(5.47722557505))\approx1.79`

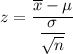
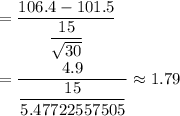
Since the calculated z > Critical z value , so we reject the null hypothesis.

We conclude that we have sufficient evidence at α = 0.05 to support the school superintendent claim that the students in her school district have an IQ higher than the average of 101.5.