Answer:
a = 129.663

Step-by-step explanation:
We know that:
T = Ia
Where T is the torque, I is the moment of inertia and a is the angular aceleration:
First, we will find the moment of inertia using the following equation:
I =
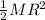
Where M is the mass and R is the radius of the disk. Replacing values, we get:
I =
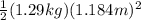
I = 0.904 kg*m^2
Second, we will find the torque using the following equation:
T = (
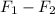 )*(R)
)*(R)
Where
 is the force on one side and
is the force on one side and
 is the force on the other side. Replacing values, we get:
is the force on the other side. Replacing values, we get:
T = (162N-63N)(1.184m)
T = 117.216N*m
Finally, we replace T and I on the initial equation as:
T = Ia
117.216N = (0.904)(a)
Solving for a:
a = 129.663
