Question

Allison is working two summer jobs, making $12 per hour lifeguarding and $8 per hour washing cars. Last week Allison worked 3 more hours lifeguarding than hours washing cars hours and earned a total of $96. Graphically solve a system of equations in order to determine the number of hours Allison worked lifeguarding last week, x , x, and the number of hours Allison worked washing cars last week, y y.

Answer 1

Allison worked 6 hours lifeguarding and 3 hours washing cars.

Explanation:

Let

Number of hours Allison worked lifeguarding last week = x

Number of hours Allison worked washing cars last week = y

1. Last week Allison worked 3 more hours lifeguarding than hours washing cars hours, then

`x-y=3`

Lifeguarding:

$12 per hour

$12x in x hours.

Washing cars:

$8 pere hour

$8y in y hours.

2. Allison earned a total of $96, hence

`12x+8y=96`

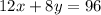
You get the system of two equations:

`\left\{\begin{array}{l}x-y=3\\ \\12x+8y=96\end{array}\right.`

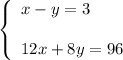
Plot the graphs of these two equations (see attached diagram). These line intersect at point (6,3), so Allison worked 6 hours lifeguarding and 3 hours washing cars.