Question

An article in the Archives of Internal Medicine reported that in a sample of 244 men, 73 had elevated total cholesterol levels (more than 200 milligrams per deciliter). In a sample of 232 women, 44 had elevated cholesterol levels. Can you conclude at the 0.05 significance level that the proportion of people with elevated cholesterol levels differs between men and women

Answer 1

Answer: We concluded that the proportion of people with elevated cholesterol levels differs between men and women.

Explanation:

Since we have given that

Hypothesis:

`H_0:p_1=p_2\\\\H_a:p_1\\eq p_2`

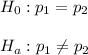
in a sample of 244 men, 73 had elevated total cholesterol level.

n₁ = 244

x₁ = 73

So,
`p_1=(x_1)/(n_1)=(73)/(244)=0.299`

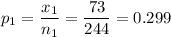
n₂ = 232

x₂ =44

So,
`p_2=(44)/(232)=0.189`

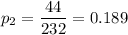
At 0.05 level of significance, z = 1.96 as it is two tail test.

So, test statistic value would be

`z=\frac{p_1-p_2}{\sqrt{(p_1(1-p_1))/(n_1)+(p_2(1-p_2))/(n_2)}}\\\\z=\frac{0.299-0.189}{\sqrt{(0.299* 0.701)/(100)+(0.189* 0.811)/(100)}}\\\\z=1.83`

Since, 1.96>1.83

Hence, we will reject the null hypothesis.

Therefore, We concluded that the proportion of people with elevated cholesterol levels differs between men and women.