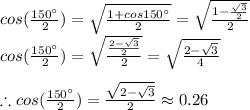Answer:
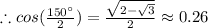
Explanation:
The given expression is
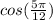
To find the exact value using identities, we can split the angle in a sum that is equivalent, that is, we rewrite the expression.
Let's rewrite the expression
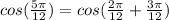
We can rewrite this way, because the sum of those fractions gives the original one. Then, we simplify

Now, here we need to transfor from radians to degrees, because that way we can obtain half-angles
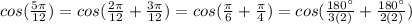
Then, we divide each fraction in a way that the final expression contains halves
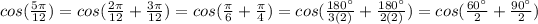
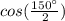
The half-angle identity is
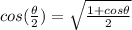
In this case,
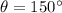 , replaing it in the identity, we have
, replaing it in the identity, we have
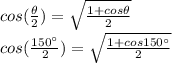
But,
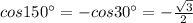 , replacing this
, replacing this