Answer:
Mean, x: 7
standard deviation(s)=0.4944
t=-3.1980
Explanation:
given data
7.4 7.0 6.5 7.4 7.6 6.2 6.9 7.6 6.5 6.9
Count, N: 10
Sum, Σx: 70
Mean, x: 7
Variance, s2: 0.24444444444444
Steps
s2 =
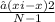
=
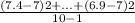
=
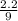
=0.24444444444444
s =
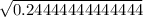
⇒s= 0.49441323247304
⇒s=0.4944
b) H0: μ = 7.5 versus Ha: μ < 7.5.
α = 0.01.
t=
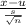
t=
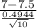
t=-3.1980
for 9 df and α = 0.01
t stat from table is -2.82
as t test is less than t
we reject the null hypothesis