Question

A student ran the following reaction in the laboratory at 311 K:CH4(g) + CCl4(g) 2CH2Cl2(g)When she introduced 4.10×10-2 moles of CH4(g) and 6.51×10-2 moles of CCl4(g) into a 1.00 liter container, she found the equilibrium concentration of CCl4(g) to be 6.03×10-2 M.Calculate the equilibrium constant, Kc, she obtained for this reaction.Kc =

Answer 1

Answer: The value of
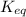`K_(eq)` is 0.044

Step-by-step explanation:

We are given:

Initial moles of methane =
`4.10* 10^(-2)mol=0.0410moles`

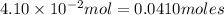
Initial moles of carbon tetrachloride =
`6.51* 10^(-2)mol=0.0651moles`

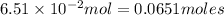
Volume of the container = 1.00 L

Concentration of a substance is calculated by:

`\text{Concentration}=\frac{\text{Number of moles}}{\text{Volume}}`

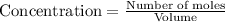
So, concentration of methane =
`(0.0410)/(1.00)=0.0410M`

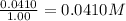
Concentration of carbon tetrachloride =
`(0.0651)/(1.00)=0.0651M`

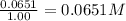
The given chemical equation follows:

`CH_4(g)+CCl_4(g)\rightleftharpoons 2CH_2Cl_2(g)`

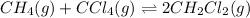
Initial: 0.0410 0.0651

At eqllm: 0.0410-x 0.0651-x 2x

We are given:

Equilibrium concentration of carbon tetrachloride =
`6.02* 10^(-2)M=0.0602M`

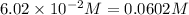
Evaluating the value of 'x', we get:

`\Rightarrow (0.0651-x)=0.0602\\\\\Rightarrow x=0.0049M`

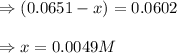
Now, equilibrium concentration of methane =
`0.0410-x=[0.0410-0.0049]=0.0361M`

Equilibrium concentration of
`CH_2Cl_2=2x=[2* 0.0049]=0.0098M`

The expression of
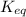`K_(eq)` for the above reaction follows:

`K_(eq)=([CH_2Cl_2]^2)/([CH_4]* [CCl_4])`

Putting values in above expression, we get:

`K_(eq)=((0.0098)^2)/(0.0361* 0.0603)\\\\K_(eq)=0.044`

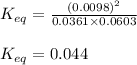
Hence, the value of
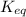`K_(eq)` is 0.044