Question

Two speed studies are taken under situations that are considered identical and the following results were obtained: • Study 1, Mean is 30.8, Standard Deviation is 6.2, and the sample size is 100 • Study 2, Mean is 32.2, Standard Deviation is 5.4, and the sample size is 200 Are the means in the two studies significantly different at the 95% confidence level?

Answer 1

Answer: No, the means in the two studies significantly is not different at the 95% confidence level.

Explanation:

Since we have given that

Study 1,

Mean = 30.8,

Standard Deviation = 6.2,

Sample size = 100

And

Study 2

Mean = 32.2,

Standard Deviation = 5.4,

Sample size = 200

So, Hypothesis would be

`H_0:\mu_1=\mu_2\\\\H_a:\mu_1\\eq \mu_2`

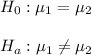
So, At 95% confidence level, z = 1.96

So, the test statistic value would be

`z=\frac{\bar{x}_1-\bar{x}_2}{\sqrt{(\sigma^2_1)/(n_1)+(\sigma^2_2)/(n_2)}}\\\\z=\frac{30.8-32.2}{\sqrt{(6.2^2)/(100)+(5.4^2)/(200)}}\\\\z=(-1.4)/(0.7281)\\\\z=-1.9228`

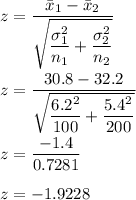
Since 1.96>-1.9228

So, we will accept the null hypothesis.

Hence,No, the means in the two studies significantly is not different at the 95% confidence level.