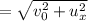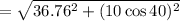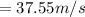Answer:
Step-by-step explanation:
Given
First stone is thrown at an angle of
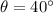 Above horizontal
Above horizontal
second stone is thrown at angle of
 below horizontal
below horizontal
let h be the height of building
Initial velocity is same in both case i.e. u=10 m/s
Horizontal velocity will remain same as there is no acceleration and there will only be vertical velocity change
for first case
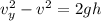
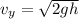
Net velocity at ground
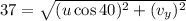

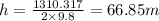
For second case
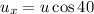
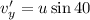
Let
 be the final vertical velocity
be the final vertical velocity
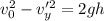
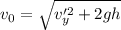
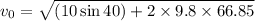
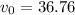
Final velocity at ground