Answer:
(a). The density of the wood is
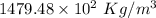
(b). The absolute pressure at the bottom of the tank is
 .
.
Step-by-step explanation:
Given that,
Side of cube = 15.0 cm
Depth = 50 cm
Tension = 6.615 N
We need to calculate the volume of the wood
Using formula of volume
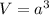
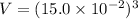

We need to calculate the density of the wood
Using buoyant force
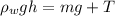
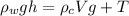
Put the value into the formula
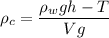
Put the value into the formula
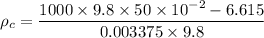
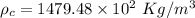
(b). We need to calculate the absolute pressure at the bottom of the tank
Using formula of absolute pressure
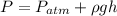
Put the value into the formula
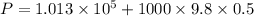
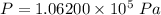
Hence, (a). The density of the wood is
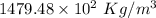
(b). The absolute pressure at the bottom of the tank is
 .
.