Question

At a local music store cd singles are sold for 6.99 and cd albums are sold for 10.99 one day there were 25 cds sold and the sales totaled 230.75 how many of each type of cd were sold

Answer 1

The number of cd singles that were sold is 11

The number of cd albums that were sold is 14

Explanation:

Given as :

The price for each cd singles = $6.99

The price for each cd albums = $10.99

The Total number of cd's sold on day = 25

The total sales amount of both cd's = $230.75

Let The numbers of cd singles = s

And The number of cd albums = a

Now, According to question

The total sales amount of both cd's = The price for each cd singles × The numbers of cd singles + The price for each cd albums × The number of cd albums

So, $6.99 × s + $10.99 × a = $230.75 .................A

And s + a = 25 ..................B

Now, solving eq A and B

I.e ( $6.99 × s + $10.99 × a ) - $6.99 × ( s + a ) = $230.75 - $6.99 × 25

Or, ( $6.99 × s - $6.99 × s ) + ( $10.99 × a - $6.99 a ) = $230.75 - $174.75

Or, 0 + 4 × a = 56

∴ a =
`(56)/(4)`

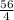
I.e a = 14

So, the number of cd albums = a = 14

Now, put the value of a in Eq B

I.e s + a = 25

Or, s = 25 - a

Or, s = 25 - 14

∴ s = 11

So, the number of cd singles = s = 11

Hence, The number of cd singles that were sold is 11 and The number of cd albums that were sold is 14 . Answer