Question

Which shows the correct substitution of the values a, b, and c from the equation 0 = 4x2 + 2x – 1 into the quadratic formula below?

Quadratic formula: x = StartFraction negative b plus or minus StartRoot b squared minus 4 a c EndRoot Over 2 a EndFraction

x = StartFraction negative 2 plus or minus StartRoot 2 squared minus 4(4)(negative 1) EndRoot Over 2(4) EndFraction
x = StartFraction negative 2 plus or minus StartRoot 2 squared minus 4(4)(1) EndRoot Over 2(4) EndFraction
x = StartFraction negative 2 plus or minus StartRoot 2 squared + 4(4)(negative 1) EndRoot Over 2(4) EndFraction

Answer 1

its B on edg2020

Explanation:

Answer 2

x = StartFraction negative 2 plus or minus StartRoot 2 squared minus 4(4)(negative 1) EndRoot Over 2(4) EndFraction

Explanation:

we know that

The formula to solve a quadratic equation of the form

`ax^(2) +bx+c=0`

is equal to

`x=\frac{-b(+/-)\sqrt{b^(2)-4ac}} {2a}`

in this problem we have

`4x^(2) +2x-1=0`

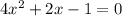
so

`a=4\\b=2\\c=-1`

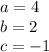
substitute in the formula

`x=\frac{-2(+/-)\sqrt{2^(2)-4(4)(-1)}} {2(4)}`

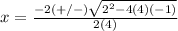
therefore

x = StartFraction negative 2 plus or minus StartRoot 2 squared minus 4(4)(negative 1) EndRoot Over 2(4) EndFraction