Question

X+1=x(x-1)
In standard form

Answer 1

Standard form of the given expression is
`x  + 1 = x ( x - 1 ) \implies  x^2 -2x - 1 = 0`

Explanation:

Here, the given expression is:

x + 1 = x ( x - 1 )

DISTRIBUTIVE PROPERTY: A(B - C) = AB - AC

Now, simplifying the given expression, we get

`x  + 1 = x ( x - 1 )  \\\implies x  + 1 = x ( x) - x(1 )  \\\implies x  + 1 = x^2  -x\\\implies x^2 -x -x - 1 = 0\\\implies x^2 -2x - 1 = 0`

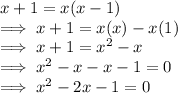
The standard form of a quadratic equation is :
`ax^2 + bx + c`

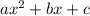
Hence, comparing the simplified expression with the Quadratic formula ,we get,
`x  + 1 = x ( x - 1 ) \implies  x^2 -2x - 1 = 0`