Question

)Suppose ABC is a right triangle with sides of lengths a, b, and c and right angle at C. Find the unknown side length using the Pythagorean theorem and then find the value of the indicated trigonometric function of the given angle. Rationalize the denominator if applicable. Find tan ???? when b=3 and c=4.

Answer 1

`a=√(7)`

`\text{tan}(A)=(√(7))/(3)`

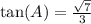
Explanation:

Please find the attachment.

We have been given that ABC is a right triangle with sides of lengths a, b, and c and right angle at C.

To find the side length a, we will Pythagoras theorem, which states that the sum of squares of two legs of a right triangle is equal to the square of the hypotenuse of right triangle.

`a^2+b^2=c^2`

Upon substituting our given values in Pythagoras theorem, we will get:

`a^2+3^2=4^2`

`a^2+9=16`

`a^2+9-9=16-9`

`a^2=7`

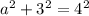
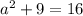
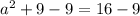
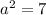
Take square root of both sides:

`a=√(7)`

Therefore, the length of side 'a' is
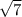`√(7)` units.

We know that tangent relates opposite side of a right triangle with adjacent side.

`\text{tan}=\frac{\text{Opposite}}{\text{Adjacent}}`

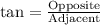
We can see that 'a' is opposite side of angle A and 'b' is adjacent side.

`\text{tan}(A)=(a)/(b)`

`\text{tan}(A)=(√(7))/(3)`

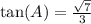
Therefore, the value of tan(A) is
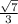`(√(7))/(3)`.