Question

A system of equations is given by 4x1 − 2x2 − 7x3 = 4 2x1 + 12x2 + 3x3 = −5 −x1 + 6x2 + 2x3 = 15 i) Write down the augmented coefficient matrix A. ii) Using row operations, put the ACM into reduced row echelon form. When doing this, you should indicate the exact row operation you are using at each stage, and the matrix it produces. You should be using the notation defined in the textbook. iii) Write down the set of equations corresponding to rref(A) and determine the set of solutions.

Answer 1

i) The augmented matrix for this system is

`\left[\begin{array}ccc4&-2&-7&4\\2&12&3&-5\\-1&6&2&15\end{array}\right]`

ii) The reduced row echelon form

`\text{rref}(A)=\left[ \begin{array}{cccc} 1 & 0 & 0 & - (692)/(65) \\\\ 0 & 1 & 0 & (423)/(130) \\\\ 0 & 0 & 1 & - (493)/(65) \end{array} \right]`

iii) The set of solutions are

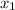`x_1` = -692/65

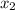`x_2` = 423/130

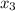`x_3` = -493/65

Explanation:

i) An augmented matrix for a system of equations is a matrix of numbers in which each row represents the constants from one equation (both the coefficients and the constant on the other side of the equal sign) and each column represents all the coefficients for a single variable.

We have the following system of equations:

`4x_1 -2x_2 - 7x_3 = 4 \\2x_1 + 12x_2 + 3x_3 = -5\\ -x_1 + 6x_2 + 2x_3 = 15`

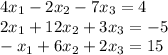
Here is the augmented matrix for this system.

`\left[\begin{array}c4&-2&-7&4\\2&12&3&-5\\-1&6&2&15\end{array}\right]`

ii) To find the reduced row echelon form of

`A=\left[ \begin{array}{cccc} 4 & -2 & -7 & 4 \\\\ 2 & 12 & 3 & -5 \\\\ -1 & 6 & 2 & 15 \end{array} \right]`

you must:

• Divide row 1 by 4
  `\left(R_1=(R_1)/(4)\right)`

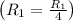
`\left[ \begin{array}{cccc} 1 & - (1)/(2) & - (7)/(4) & 1 \\\\ 2 & 12 & 3 & -5 \\\\ -1 & 6 & 2 & 15 \end{array} \right]`

• Subtract row 1 multiplied by 2 from row 2
  `\left(R_2=R_2-\left(2\right)R_1\right)`

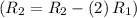
`\left[ \begin{array}{cccc} 1 & - (1)/(2) & - (7)/(4) & 1 \\\\ 0 & 13 & (13)/(2) & -7 \\\\ -1 & 6 & 2 & 15 \end{array} \right]`

• Add row 1 to row 3
  `\left(R_3=R_3+R_1\right)`

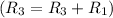
`\left[ \begin{array}{cccc} 1 & - (1)/(2) & - (7)/(4) & 1 \\\\ 0 & 13 & (13)/(2) & -7 \\\\ 0 & (11)/(2) & (1)/(4) & 16 \end{array} \right]`

• Divide row 2 by 13
  `\left(R_2=(R_2)/(13)\right)`

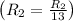
`\left[ \begin{array}{cccc} 1 & - (1)/(2) & - (7)/(4) & 1 \\\\ 0 & 1 & (1)/(2) & - (7)/(13) \\\\ 0 & (11)/(2) & (1)/(4) & 16 \end{array} \right]`

• Add row 2 multiplied by 1/2 to row 1
  `\left(R_1=R_1+\left((1)/(2)\right)R_2\right)`

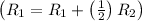
`\left[ \begin{array}{cccc} 1 & 0 & - (3)/(2) & (19)/(26) \\\\ 0 & 1 & (1)/(2) & - (7)/(13) \\\\ 0 & (11)/(2) & (1)/(4) & 16 \end{array} \right]`

• Subtract row 2 multiplied by 11/2 from row 3

`\left[ \begin{array}{cccc} 1 & 0 & - (3)/(2) & (19)/(26) \\\\ 0 & 1 & (1)/(2) & - (7)/(13) \\\\ 0 & 0 & - (5)/(2) & (493)/(26) \end{array} \right]`

• Multiply row 3 by −2/5
  `\left(R_3=\left(- (2)/(5)\right)R_3\right)`

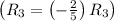
`\left[ \begin{array}{cccc} 1 & 0 & - (3)/(2) & (19)/(26) \\\\ 0 & 1 & (1)/(2) & - (7)/(13) \\\\ 0 & 0 & 1 & - (493)/(65) \end{array} \right]`

• Add row 3 multiplied by 3/2 to row 1
  `\left(R_1=R_1+\left((3)/(2)\right)R_3\right)`

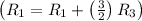
`\left[ \begin{array}{cccc} 1 & 0 & 0 & - (692)/(65) \\\\ 0 & 1 & (1)/(2) & - (7)/(13) \\\\ 0 & 0 & 1 & - (493)/(65) \end{array} \right]`

• Subtract row 3 multiplied by 1/2 from row 2
  `\left(R_2=R_2-\left((1)/(2)\right)R_3\right)`

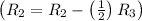
`\left[ \begin{array}{cccc} 1 & 0 & 0 & - (692)/(65) \\\\ 0 & 1 & 0 & (423)/(130) \\\\ 0 & 0 & 1 & - (493)/(65) \end{array} \right]`

The answer is

`\text{rref}(A)=\left[ \begin{array}{cccc} 1 & 0 & 0 & - (692)/(65) \\\\ 0 & 1 & 0 & (423)/(130) \\\\ 0 & 0 & 1 & - (493)/(65) \end{array} \right]`

iii) The set of solutions are

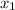`x_1` = -692/65

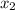`x_2` = 423/130

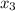`x_3` = -493/65