Question

a right circular cone has a height of 18 and a base radius of 12. A slice parallel to the base in made completely throught the cone, and the resulting smaller cone has a volume that is 1/2 the volume of the original cone. What is the height of the smaller cone?

Answer 1

Height of smaller cone is 14.29

Explanation:

`\texttt{Volume of cone, V = }(1)/(3)\pi r^2h`

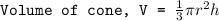
For the first cone

Height, h = 18

Radius, r = 12

Substituting

`\texttt{Volume of cone, V = }(1)/(3)\pi r^2h\\\\\texttt{Volume of cone, V = }(1)/(3)* \pi * 12^2* 18=2714.34`

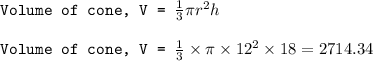
Volume of new cone formed is half of the older cone.

Volume of new cone = 0.5 x 2714.34 = 1357.17

For the cone as the height reduces to 18 radius reduces to zero.

`tan\theta =(12)/(18)\\\\\theta =33.7^0`

`\texttt{Volume of new cone = }(1)/(3)\pi r_1^2h_1\\\\tan\theta =(r_1)/(h_1)\Rightarrow r_1=h_1tan\theta\Rightarrow r_1=h_1tan33.7=0.667h_1\\\\\texttt{Volume of new cone = }(1)/(3)\pi * (0.667h_1)^2h_1=0.467h_1^3`

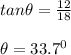
We have

0.467h₁³ = 1357.17

h₁ = 14.29

Height of smaller cone = 14.29