Question

keith is the leading goal scorer for a team in an hockey league. last season he scored 42 goals in 82 games. assuming he scores goals at a constant rate what is the slope of line that represents this relationship if the number of games is along the x-axis and the number of goals is along the y-axis

Answer 1

0.512 goals per game

Explanation:

Given:

The number of games is represented by 'x' and number of goals is represented by 'y'.

Now, 'y' varies directly with x and at a constant rate.

A direct relationship line is given as:

`y=mx`

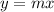
Where, 'm' is the constant rate of change.

Now, for
`x=82,y=42`

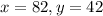
So, a point on the line is given as (82, 42).

Plug in the given values in the above equation and solve for 'm'. This gives,

`42=82m\\m=(42)/(82)\\m=0.512`

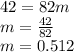
Therefore, Keith scores at a constant rate of 0.512 goals per game.