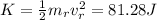Answer:
If the rifle is held loosely away from the shoulder, the recoil velocity will be of -8.5 m/s, and the kinetic energy the rifle gains will be 81.28 J.
Step-by-step explanation:
By momentum conservation, and given the bullit and the recoil are in a straight line, the momentum analysis will be unidimentional. As the initial momentum is equal to zero (the masses are at rest), we have that the final momentum equals zero, so
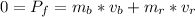
now we clear
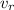 and use the given data to get that
and use the given data to get that
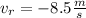
But we have to keep in mind that the bullit accelerate from rest to a speed of 425 m/s, then if the rifle were against the shoulder, the recoil velocity would be a fraction of the result obtained, but, as the gun is a few centimeters away from the shoulder, it is assumed that the bullit get to its final velocity, so the kick of the gun, gets to its final velocity
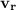 too.
too.
Finally, using
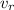 we calculate the kinetic energy as
we calculate the kinetic energy as