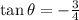Question

Look at the figure below.

Answer 1

∴
`\tan \theta = -(3)/(4)`

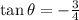
Explanation:

Let the triangle name as Δ ABO a right triangle at ∠ B =90°

Such that,

OA = radius

AB = y coordinate = 12

BO = x coordinate = 16 (positive because distance cannot be in negative)

To Find:

`\tan \theta=?`

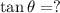
Solution:

In right triangle Δ ABO ,By Pythagoras theorem we get the radius,

`(\textrm{Hypotenuse})^(2) = (\textrm{Shorter leg})^(2)+(\textrm{Longer leg})^(2)`

`r^(2) = 16^(2)+12^(2)\\\\r^(2) =400\\\therefore r = 20\ units`

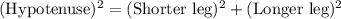
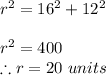
∴ OA = 20

OB = 16

Also tan (180 -θ) = - tan (θ)

Now In right triangle Δ ABO

m∠ AOB = 180 -θ

∴
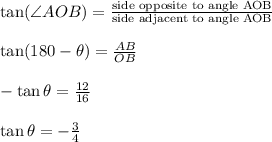
`\tan (\angle AOB) = \frac{\textrm{side opposite to angle AOB}}{\textrm{side adjacent to angle AOB}}\\\\\tan (180 -\theta) = (AB)/(OB)\\\\-\tan \theta =(12)/(16) \\\\\tan \theta = -(3)/(4)`

∴
`\tan \theta = -(3)/(4)`