Question

Matt and Trey are remodeling their gardens. Matt purchased 8 ferns and 1 rosebush for $35. Trey purchased 4 ferns and 3 rosebushes for $25. Determine the price of each plant.

Answer 1

Cost of a fern = $4

cost of a rose bush = $3

Explanation:

Let cost of a fern in dollars be =
`x`

Let cost of a rosebush in dollars be =
`y`

Matt purchased 8 ferns and 1 rosebush for $35

Cost of 8 ferns in dollars will be =
`8x`

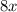
cost of a rosebush in dollars is =
`y`

Total cost of 8 ferns and 1 rosebush in dollars =
`8x+y`

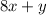
So, we have a Matt's equation as:

`8x+y=35`

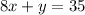
Trey purchased 4 ferns and 3 rosebushes for $25.

Cost of 4 ferns in dollars =
`4x`

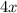
Cost of 3 rosebushes in dollars =
`3y`

Total cost of 4 ferns and 3 rosebush in dollars =
`4x+3y`

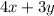
So, we have a Trey's equation as:

`4x+3y=25`

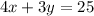
The system of equations is :

A)
`8x+y=35`

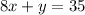
B)
`4x+3y=25`

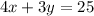
Solving the system by substitution method.

Rearranging equation A, to solve for
`y` in terms of
`x`

Subtracting both sides by
`8x`

`8x+y-8x=35-8x`

`y=35-8x`

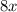
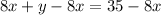
Substituting value of
`y` we got from A into equation B.

`4x+3(35-8x)=25`

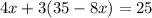
Using distribution.

`4x+105-24x=25`

Simplifying.

`-20x+105=25`

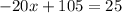
Subtracting both sides by 105.

`-20x+105-105=25-105`

`-20x=-80`

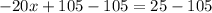
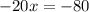
Dividing both sides by -20.

`(-20x)/(-20)=(-80)/(-20)`

∴
`x=4`

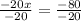
We can plugin
`x=4` in the rearranged equation A to get value of
`y`

`y=35-8(4)`

`y=35-32`

∴
`y=3`

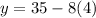
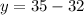
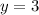
Cost of a fern = $4

Cost of a rosebush = $3