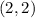Answer:
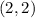
Explanation:
1. Substitute
 into first equation and solve for "x" in order to find the x-intercept of the first line:
into first equation and solve for "x" in order to find the x-intercept of the first line:

2. Substitute
 into the first equation and solve for "y" in order to find the y-intercept of the first line:
into the first equation and solve for "y" in order to find the y-intercept of the first line:

Knowing that first line passes through the points
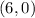 and
and
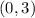 , you can graph it.
, you can graph it.
3. Substitute
 into second equation and solve for "x" in order to find the x-intercept:
into second equation and solve for "x" in order to find the x-intercept:
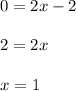
4. Substitute
 into the second equation and solve for "y" in order to find the y-intercept of the second line:
into the second equation and solve for "y" in order to find the y-intercept of the second line:
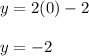
Knowing that second line passes through the points
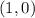 and
and
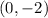 , you can graph it.
, you can graph it.
The solution of the system of equations is the point of intersection between the lines. Therefore, the solution of this system is: