Answer:
option (c)
Step-by-step explanation:
Fundamental frequency of segment A = f
Second harmonic frequency of B = fundamental frequency of A .
Tension in both the wires is same and the mass density is also same as the wires are identical.
fundamental frequency of wire A is given by
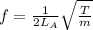 .... (1)
.... (1)
Second harmonic of B is given by
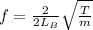 .... (2)
.... (2)
Equation (1) is equal to equation (2), we get
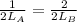

So, LB = 2 L
Thus, the length of wire segment B is 2 times the length of wire segment A.