Question

During World War II, tritium (3H) was a component of fluorescent watch dials and hands. Assume you have such a watch that was made in January 1944. If 16% or more of the original tritium was needed to read the dial in dark places, until what year could you read the time at night? (For 3H, t1/2 = 12.3 yr.)

Answer 1

1976

Step-by-step explanation:

The first order decay of tritium can be represented through the following expression.

`ln(([H]_(t))/([H]_(0)) )=-k.t`

where,

[H]t is the concentration of tritium after a time t has elapsed

[H]₀ is the initial concentration of tritium

k is the rate constant

Given the half-life (t1/2) is 12.3 years, we can calculate the rate constant using the following expression.

`k=(ln2)/(t_(1/2)) =(ln2)/(12.3y) =0.0564y^(-1)`

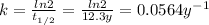
The concentration of tritium at certain time is 16% of the initial concentration, that is, [H]t = 0.16 [H]₀.

`ln((0.16[H]_(0))/([H]_(0)) )=-0.0564y^(-1).t\\t=32y`

If the watch was made in 1944, you could read the time until 1944 + 32 = 1976.