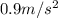Question

A model car is propelled by a cylinder of carbon dioxide gas. The cylinder emits gas at a rate of 4.5 g/s with an exit speed of 80.0 m/s. The car has a mass of 400 g, including the CO2 cylinder. Starting from rest, what is the car’s initial acceleration?

Answer 1

In order to solve this problem, it is necessary to apply the concepts related to the Force by the execution of material given between the mass flow and the velocity, against the force caused by the acceleration against the net mass. Mathematically this can be expressed as:

`F_m = F_i`

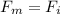
Where,

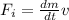`F_i = (dm)/(dt) v` Force per mass flow pulse

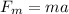`F_m = ma` Force by acceleration

In this way matching both expressions we would have to

`ma = (dm)/(dt)v`

`a = (dm)/(dt) (v)/(m)`

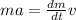
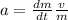
Our values are given as

`(dm)/(dt) = 0.0045kg/s`

`v = 80m/s`

`m = 0.4Kg`

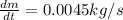
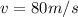
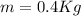
Replacing we have that the value of acceleration is,

`a = (0.0045*80)/(0.4)`

`a = 0.90m/s^2`

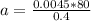
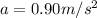
Therefore the car's acceleration is
`0.9m/s^2`