Question

A 1,492.3-kg airplane travels down the runway. Each of its four engines provides a force of

1,447.5 N. Find the acceleration of the airplane, in m/s2. (Ignore friction.)

Answer 1

The acceleration of the air plane is
`3.879 \mathrm{m} / \mathrm{s}^(2)`

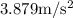
Step-by-step explanation:

Given:

The mass of the air plane = 1492.3 kg

Force of each four engine = 1447.5 N

So, the total force of four engines can be calculated as = 4(1447.5) = 5790 N

The force that acts on the object is equal to the product of mass (m) and its acceleration. It can express by the below formula,

`\text {Force }(F)=m * \text { acceleration }(a)`

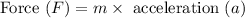
The above equation can be written as below to find acceleration,

`a=(F)/(m)`

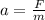
Now. Substitute the given values, we get,

`a=(5790)/(1492.3)=3.879 \mathrm{m} / \mathrm{s}^(2)`