Question

The head of public safety notices that the average driving speed at a particular intersection averages μ = 35 mph with a standard deviation of σ = 7.5 mph. After a school speed limit sign of 20 mph is placed at the intersection, the first 40 cars travel past at an average speed of 32 mph. Using the .01 significance level, was there a significant change in driving speed?

a. Use the five steps of hypothesis testing (report results in APA format).

b. Sketch the distributions involved.

c. Figure the confidence limits for the 99% confidence interval.

Answer 1

The answer is C because its the only one that makes sense when you see what the question is asking you

Answer 2

a. With a calculated t-value of t_(39) = -1.93 and a critical t-value of ±2.71 at a .01 significance level (two-tailed test), we fail to reject the null hypothesis. There isn't enough evidence to conclude a significant change in driving speed after the installation of the school speed limit sign.

c. The 99% confidence interval for the mean difference in driving speed is (-4.67, 0.67) mph.

Explanation:

a. To conduct the hypothesis test, we set up the null hypothesis H₀: μ₁ - μ₂ = 0 (there's no change in driving speed) against the alternative hypothesis H₁: μ₁ - μ₂ ≠ 0 (there's a change in driving speed). Given the sample mean difference of
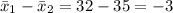`\(\bar{x}_1 - \bar{x}_2 = 32 - 35 = -3\)` mph, with a sample size (n) of 40 and a standard deviation (σ) of 7.5 mph, the calculated t-value is
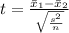`\(t = \frac{\bar{x}_1 - \bar{x}_2}{\sqrt{(s^2)/(n)}}\)`, where s is the pooled standard deviation. The calculated t-value is -1.93. Comparing this to the critical t-value of ±2.71 (two-tailed test) at a .01 significance level and degrees of freedom df = 39, we fail to reject the null hypothesis.

c. The 99% confidence interval for the mean difference in driving speed is calculated using the formula
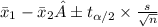`\(\bar{x}_1 - \bar{x}_2 ± t_(\alpha/2) * (s)/(√(n))\)`, where
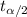`\(t_(\alpha/2)\)` is the critical value at a 99% confidence level. For a two-tailed test at α = 0.01 and degrees of freedom df = 39, the critical t-value is ±2.71. Plugging in the values, we find the confidence interval for the mean difference in driving speed to be (-4.67, 0.67) mph. This interval includes zero, further supporting the lack of a significant change in driving speed after the installation of the school speed limit sign.