To solve this problem it is necessary to apply the kinematic equations of movement description, where the speed of a body is defined as the distance traveled in a given time, that is to say

where,
x = Displacement
t = time
Since the moon is making a path equal to that of a circle, we know by geometry that the perimeter of a circle is given by
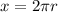
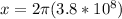
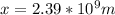
At the same time we have that time is equal to
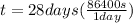
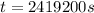
Using the equation for velocity we have finally that

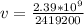
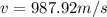
Therefore the speed of the Moon in its orbit is 987.92m/s