Step-by-step explanation:
Given that,
Area enclosed by a brass bracelet,
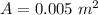
Initial magnetic field,
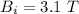
The electrical resistance around the circumference of the bracelet is, R = 0.02 ohms
Final magnetic field,
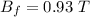
Time,
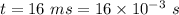
The expression for the induced emf is given by :
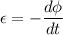
 = magnetic flux
= magnetic flux
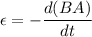
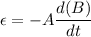
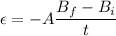
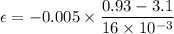
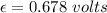
So, the induced emf in the bracelet is 0.678 volts.
Using ohm's law to find the induced current as :
V = IR
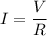
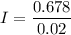
I = 33.9 A
or
I = 34 A
So, the induced current in the bracelet is 34 A. Hence, this is the required solution.