Question

Calculate the temperature increase in a 1.00-kg sample of water that results from the conversion of gravitational potential energy directly to heat energy in the one of the world's tallest waterfall on height 807 m. (Express your answer to three significant figures.)

Answer 1

To solve this problem it is necessary to apply the concepts concerning the conservation of both potential and thermodynamic energy of the body. That is to say that as the body has a loss of potential energy it is gained in the form of thermal energy on water. If the potential energy is defined as

`PE = mgh`

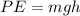
Where,

m= mass

g = Gravitational acceleration

h = Height

And thermal energy is obtained as

`Q = mC_p\Delta T`

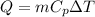
Where,

`\Delta T` = Change in Temperature

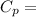`C_p =` Specific Heat

m = Mass

We can equate this equation and rearrange to find the change at the Temperature, then

`mgh = mC_p\Delta T`

`\Delta T = (gh)/(C_p)`

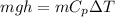
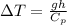
Our values are given as,

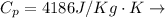`C_p = 4186J/Kg\cdot K \rightarrow` Specific Heat Water

Using energy conservation

`g = 9.8m/s^2`

`h = 807m`

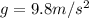
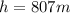
Replacing,

`\Delta T = ((9.8)(807))/(4186)`

`\Delta T = 1.89K`

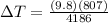
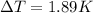
Therefore the temperature increase in a 1kg sample of water is 1.89K