Answer:
116.7 Hz
Step-by-step explanation:
Let there are two wires A and B.
Tension in wire A = T
Tension in wire B = 2T
Length of wire A = L
Length of wire B = 2L
fundamental frequency in wire A, fA = 330 Hz
let the fundamental frequency in wire B is fB.
The formula for the fundamental frequency is given by

where, μ is the mass per unit length
mass per unit length of wire A = Area of wire A x density
mass per unit length of wire B = Area of wire B x density

So,
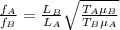
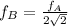
fB = 330 / 2.828
fB = 116.7 Hz
Thus, the frequency in the second wire is 116.7 Hz.