Step-by-step explanation:
It is given that,
Mas of the car,
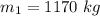
Initial speed of the car,
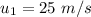
Mass of the truck,
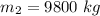
Initial speed of the car,
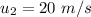
Final speed of the car,
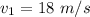
(a) It is a case of elastic collision. Let
 is the final velocity of the truck right after the collision. Using the conservation of linear momentum to find it :
is the final velocity of the truck right after the collision. Using the conservation of linear momentum to find it :
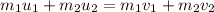
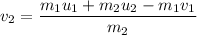
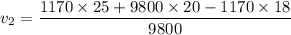
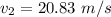
(b) Initial kinetic energy is given by :
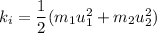
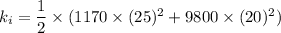

Final kinetic energy is given by :
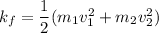
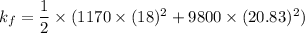
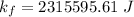
The change in mechanical energy of the car truck system in the collision:
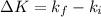
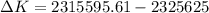
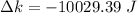
The loss in kinetic energy is 10029.39 Joules.
(c) The change in mechanical energy gets changed energy gets changed in the form of heat and light.
Hence, this is the required solution.