Question

Consider an asset that costs $120 today. You are going to hold it for 1 year and then sell it. Suppose that there is a 25 percent chance that it will be worth $100 in a year, a 25 percent chance that it will be worth $115 in a year, and a 50 percent chance that it will be worth $140 in a year. What is its average expected rate of return?

At what price would the asset have a zero rate of return?

Answer 1

Average expected rate of return is 3.13%

The asset have a zero rate of return if at price of $120

Step-by-step explanation:

Rate of return RR =
`(Future\:Value - Initial\:Value)/(Initial\:Value) * 100`

Rate of return of the first possibility: (100-120)/120 * 100 = -16.67%

Rate of return of the second possibility: (115-120)/120 * 100 = -4.16%

Rate of return of the third possibility: (140-120)/120 * 100 = 16.67%

Average expected rate of return =
`\sum{weight_(i)RR_(i)}`

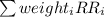
= 0.25*(-16.67%) + 0.25*(-4.16%) + 0.5*16.67% = 3.13%

RR = 0 => Future Value - Initial Value = 0

The asset have a zero rate of return when future price is the same as current price ($120)

Answer 2

1. the average expected rate of return = 3.13%
2. the current price at which the asset would have a zero rate of return is $123.75

Step-by-step explanation:

To determine the expected rate of return we must first calculate the expected future value of the asset:

$100 x 25% = $25.00

$115 x 25% = $28.75

$140 x 50% = $70.00

the expected future value = $25.00 + $28.75 + $70.00 = $123.75

the average expected return = $123.75 - $120 = $3.75

the average expected rate of return = ($3.75 / $120) x 100 = 3.13%

the current price at which the asset would have a zero rate of return is $123.75, since the average expected return = $123.75 - $123.75 = 0