Question

A pig farm has 1000 feet of fence, but the 4 different pigs must be kept in separate pins. There is also a road along one edge and a fence along the road is not needed. What are the dimensions needed to maximize the area of each pin? What is the area for each pin? This is a quadratic test by the way, please help!

Answer 1

The Dimensions of each pin are
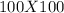`100 X 100` ft in square shape.

The area of each pin is
`A = (100)^(2) = 10000 ft^(2)`

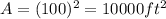
Explanation:

It is given that the total length of fence is 1000 feet.

The let the measure of each side of fence pin be "x" , as shown in the figure.

The total sum of the length is
`10x`.

This,
`10x = 1000`

`x = 100 ft`

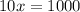
Thus the dimensions of each side of pin is 100 ft.

The area of square is given by,
`A = x^(2) = (100)^(2) = 10000 ft^(2)`

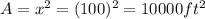
Thus the area of each symmetric pin is 10000
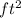`ft^(2)`.