Question

A telescope can be used to enlarge the diameter of a laser beam and limit diffraction spreading. The laser beam is sent through the telescope in opposite the normal direction and can then be projected onto a satellite or the Moon. If this is done with the Hale telescope, producing a 5.08 m diameter beam of 613 nm light, what is the minimum angular spread of the beam?

Answer 1

Angular spread,
`\theta=1.472* 10^(-7)\ rad`

Step-by-step explanation:

It is given that,

Wavelength of the light,
`\lambda=613\ nm=613* 10^(-9)\ m`

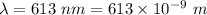
Diameter of the telescope, D = 5.08 m

The minimum angular spread is given by :

`\theta=(1.22\lambda)/(D)`

`\theta=(1.22* 613* 10^(-9))/(5.08)`

`\theta=1.472* 10^(-7)\ rad`

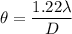
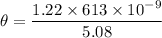
So, the minimum angular spread of the beam is
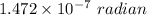`1.472* 10^(-7)\ radian`. Hence, this is the required solution.