Question

A 15.0-μF capacitor is charged by a 130.0-V power supply, then disconnected from the power and connected in series with a 0.280-mH inductor. Part A Calculate the oscillation frequency of the circuit. Express your answer with the appropriate units.

Answer 1

The resonant frequency of a circuit is the frequency
`\omega_0` at which the equivalent impedance of a circuit is purely real (the imaginary part is null).

Mathematically this frequency is described as

`f = (1)/(2\pi)(\sqrt{(1)/(LC)})`

Where

L = Inductance

C = Capacitance

Our values are given as

`C = 15*10^(-6)\mu F`

`L = 0.280*10^(-3)mH`

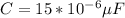
Replacing we have,

`f = (1)/(2\pi)(\sqrt{(1)/(LC)})`

`f = (1)/(2\pi)(\sqrt{(1)/((15*10^(-6))(0.280*10^(-3)))})`

`f= 2455.81Hz`

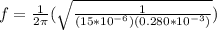
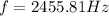
From this relationship we can also appreciate that the resonance frequency infers the maximum related transfer in the system and that therefore given an input a maximum output is obtained.

For this particular case, the smaller the capacitance and inductance values, the higher the frequency obtained is likely to be.