Question

Changes in airport procedures require considerable planning. Arrival rates of aircrft are important factors that muct be taken into account. Suppose small aircraft arrive at a certain airport, according to a Poisson process, at the rate of 5.5 per hour(a) What is the probability that exactly 4 small aircraft arrive during a 1-hour period?(b) What is the probability that at least 4 arrive duringa 1-hour period?(c) If we define a working day as 12 hours, what isthe probability that at least 75 small aircraft arrive during a working day?

Answer 1

a) 0.1558

b) 0.7983

c) 0.1478

Explanation:

If we suppose that small aircraft arrive at the airport according to a Poisson process at the rate of 5.5 per hour and if X is the random variable that measures the number of arrivals in one hour, then the probability of k arrivals in one hour is given by:

`\bf P(X=k)=\displaystyle((5.5)^ke^(-5.5))/(k!)`

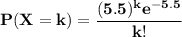
(a) What is the probability that exactly 4 small aircraft arrive during a 1-hour period?

`\bf P(X=4)=\displaystyle((5.5)^4e^(-5.5))/(4!)=0.1558`

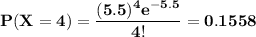
(b) What is the probability that at least 4 arrive during a 1-hour period?

`\bf P(X\geq4)=1-P(X<4)=1-(P(X=0)+P(X=1)+P(X=2)+P(X=3))=\\\\=1-\left(e^(-5.5)+(5.5)e^(-5.5)+\displaystyle((5.5)^2e^(-5.5))/(2!)+\displaystyle((5.5)^3e^(-5.5))/(3!) \right)=0.7983`

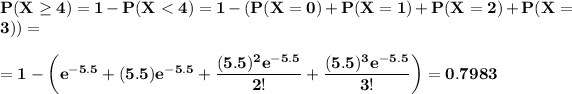
(c) If we define a working day as 12 hours, what is the probability that at least 75 small aircraft arrive during a working day?

If we redefine the time interval as 12 hours instead of one hour, then the rate changes from 5.5 per hour to 12*5.5 = 66 per working day, and the pdf is now

`\bf P(X=k)=\displaystyle((66)^ke^(-66))/(k!)`

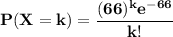
and we want P(X ≥ 75) = 1-P(X<75). But

`\bf P(X<75)=\displaystyle\sum_(k=0)^(74)\displaystyle((66)^ke^(-66))/(k!)=0.852`

hence

P(X ≥ 75) = 1-0.852 = 0.1478