Answer:
Value of
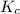 for the given reaction is 7.7
for the given reaction is 7.7
Step-by-step explanation:
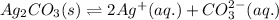
![K_(sp)(Ag_(2)CO_(3))=[Ag^(+)]^(2)[CO_(3)^(2-)]](https://img.qammunity.org/2020/formulas/chemistry/college/qu09rohnkg5r8dolc61xkhdvphgsgtt41p.png)
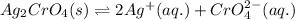
![K_(sp)(Ag_(2)CrO_(4))=[Ag^(+)]^(2)[CrO_(4)^(2-)]](https://img.qammunity.org/2020/formulas/chemistry/college/4sjx1x0tior7ep70oml8tv24gpnmdvoxqz.png)
Where
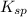 represents solubility product
represents solubility product
For the given reaction,
![K_(c)=([CO_(3)^(2-)])/([CrO_(4)^(2-)])](https://img.qammunity.org/2020/formulas/chemistry/college/rva0r1iyxdvwmxqqyy7zx2zgji4vwar6sv.png) (concentration of pure solids remain constant during reaction. Hence their concentration is taken as 1 to exclude them from equilibrium constant expression)
(concentration of pure solids remain constant during reaction. Hence their concentration is taken as 1 to exclude them from equilibrium constant expression)
So,
![K_(c)=([Ag^(+)]^(2)[CO_(3)^(2-)])/([Ag^(+)]^(2)[CrO_(4)^(2-)])](https://img.qammunity.org/2020/formulas/chemistry/college/c25dn2sb6qir04jfw8eysmqe75m54rpk0i.png)
or,
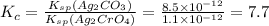
Hence option (B) is correct