Question

The yearly amounts of carbon emissions from cars in Belgium are normally distributed with a mean of 13.9 gigagrams per year and a standard deviation of 9.2 gigagrams per year. Find the probability that the amount of carbon emissions from cars in Belgium for a randomly selected year are between 12.8 gigagrams and 14.0 gigagrams per year.

0.052
0.548
0.452
0.519

Answer 1

Answer: 0.052

Explanation:

Given : The yearly amounts of carbon emissions from cars in Belgium are normally distributed with a mean of 13.9 gigagrams per year and a standard deviation of 9.2 gigagrams per year.

i.e.
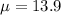`\mu=13.9` and
`\sigma=9.2`

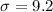
Let x denotes the yearly amounts of carbon emissions from cars in Belgium.

Then, the probability that the amount of carbon emissions from cars in Belgium for a randomly selected year are between 12.8 gigagrams and 14.0 gigagrams per year will be :-

`P(12.8<x<14.0)=P((12.8-13.9)/(9.2)<(x-\mu)/(\sigma)<(14.0-13.9)/(9.2))\\\\=P(-0.12<z<0.01)\ \ [\because\ z=(x-\mu)/(\sigma)]\\\\=P(z<0.01)-P(z<-0.12)\\\\=P(z<0.01)-(1-P(z<0.12))\ \ [\because P(Z<-z)=1-P(z<z)]\\\\=0.5040-(1-0.5478)\ \ [\text{By using z-table}]\\\\\=0.5040-0.4522=0.0518\approx0.052`

Hence, the required probability = 0.052