Question

Titanium and chlorine react to form titanium(IV) chloride, like this: Ti(s) + 2 Cl 2(g)-TiCl 4( At a certain temperature, a chemist finds that a 7.0 L reaction vessel containing a mixture of titanium, chlorine, and titanium(IV) chloride at equilibrium has the following composition compound amount 1.67 g Cl 2.93 g TiCI 2.02 g Ti Calculate the value of the equilibrium constant K for this reaction. Round your answer to 2 significant digits.

Answer 1

Answer: The value of equilibrium constant for the reaction is
`8.5* 10^(7)`

Step-by-step explanation:

The given chemical equation follows:

`Ti(s)+2Cl_2(g)\rightarrow TiCl_4(l)`

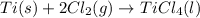
The expression of
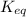`K_(eq)` for the above reaction follows:

`K_(eq)=(1)/([Cl_2]^2)`

Concentration of pure solids and liquids are taken as 1 in the equilibrium constant expression.

Thus, titanium and titanium tetrachloride does not appear in the expression.

We are given:

Equilibrium amount of titanium = 2.93 g

Equilibrium amount of titanium tetrachloride = 2.02 g

Equilibrium amount of chlorine gas = 1.67 g

To calculate the number of moles, we use the equation:

`\text{Number of moles}=\frac{\text{Given mass}}{\text{Molar mass}}`

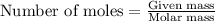
Given mass of chlorine gas = 1.67 g

Molar mass of chlorine gas = 71 g/mol

Putting values in above equation, we get:

`\text{Moles of chlorine gas}=(1.67g)/(71g/mol)=0.024mol`

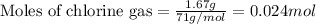
Volume of vessel = 7.0 L

Concentration of a substance is calculated by:

`\text{Concentration}=\frac{\text{Number of moles}}{\text{Volume}}`

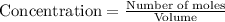
So, concentration of chlorine gas =
`(0.024)/(7.00)=3.23* 10^(-3)M`

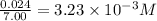
Putting the value in equilibrium constant expression, we get:

`K_(eq)=(1)/((3.43* 10^(-3))^2)\\\\K_(eq)=8.5* 10^(7)`

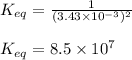
Hence, the value of equilibrium constant for the reaction is
`8.5* 10^(7)`