Answer:
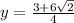 and
and
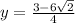
y = StartFraction 3 + 6 StartRoot 2 EndRoot Over 4 EndFraction and y = StartFraction 3 minus 6 StartRoot 2 EndRoot Over 4 EndFraction
Explanation:
The given quadratic equation is (4y - 3)² = 72
We have to solve this equation for y.
Now, 4y - 3 = ± 6√2
⇒ 4y = 3 ± 6√2
⇒
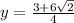 and
and
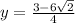
Therefore, the solution is y = StartFraction 3 + 6 StartRoot 2 EndRoot Over 4 EndFraction and y = StartFraction 3 minus 6 StartRoot 2 EndRoot Over 4 EndFraction (Answer)