Question

What is the perimeter of the figure​

Answer 1

The perimeter of the figure is 111.46 units

Explanation:

Given:

RS = 43

LS = 18√2

A right Triangle is attached to a Rectangle.

A right Triangle is having measure angle 45° , 90°

and Hypotenuse = 18√2

∴ The Third Angle measure will also be 45° {angles Sum property of a triangle}

∴ the right angled triangle is an Isosceles triangle.

∴ Two sides are equal LT = TS

To Find:

Perimeter of figure = ?

Solution:

we have

`\sin 45 = \frac{\textrm{side opposite to angle 45}}{Hypotenuse}\\`

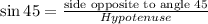
we Know sin 45 = 1/√2

∴
`(1)/(√(2) )= (LT)/(18√(2))\\\\\therefore LT = 18\ unit\\\\\therefore TS = 18\ unit\\`

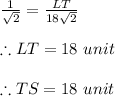
Now ,

ARTL is a Rectangle

∴ opposite side of a rectangle are equal

∴ LT = AR = 18 unit

and AL = RT

But,

RT = RS - TS

= 43 - 18

25

∴ AL = RT = 25

∴ Perimeter of figure = AL + LS + RS + AR

= 25 + 18√2 + 43 + 18

= 86 + 18√2

= 111.455

= 111.46 units

∴ Perimeter of figure = 111.46 units