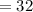Answer:
The measure of center would this student want his teacher to use is the
median

Mean
 , Mode
, Mode
 , Range
, Range
 and Interquartile Range
and Interquartile Range
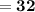
Explanation:
Given Data set

Number of elements in data set

To find Mean
The ‘Mean” is the average of a set of numbers.
The "Mean" is computed by adding all of the numbers in the data together and dividing by the number of elements contained in the data set.
Mean
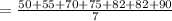
Mean
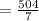
Mean
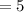
Median
The “Median” is the middle value of a set of ordered numbers.
Therefore Median
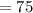
Mode
The "Mode" for a set of data is the value that occurs most often.
It is not uncommon for a data set to have more than one mode. This happens when two or more elements occur with equal frequency in the data set.
Therefore Mode
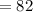
Range
The "Range" is the difference between the largest value and smallest value in a set of data.
Range

Range
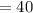
Interquartile Range
The “Interquartile Range” is the difference between smallest value and the largest value of the middle 50% of a set of data.
The "Interquartile Range" is from Q1 to Q3:
To find the interquartile range of a set of data:
The cut the list into four equal parts
. The quartiles are the “cuts”
The interquartile range is the distance between the two middle sets of data
Interquartile Range
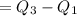
Interquartile Range
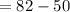
Interquartile Range