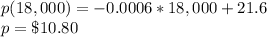Question

A baseball team plays in a stadium that holds 52000 spectators. With the ticket price at $9 the average attendance has been 21000. When the price dropped to $6, the average attendance rose to 26000.

a) Find the demand function p(x), where x is the number of the spectators. (Assume p(x) is linear.)
b) How should ticket prices be set to maximize revenue?

Answer 1

a) p(x)=-0.0006x +21.6

b) $10.80

Explanation:

a) Assuming that p(x) is linear, the slope can be found by:

`m=(\$9-\$6)/(21000-26000) \\m=-0.0006`

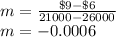
Applying the point (21000; $9) to the general linear equation gives us the demand function:

`(p-p_0)=m(x-x_0)\\(p-9)=-0.0006(x-21,000)\\p(x)=-0.0006x +21.6`

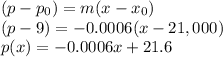
b) Revenue is given by the number of tickets sold multiplied by the price, the revenue function is:

`R(x) = xp(x)\\R(x) = -0.0006x^2 +21.6x`

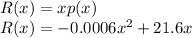
The value of x for which the revenue function's derivate is zero is the number of spectators that yield the maximum revenue:

`(dR(x))/(dx) = -0.0012x +21.6 = 0\\x=(21.6)/(0.0012)\\x= 18,000`

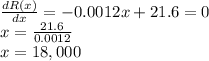
At x = 18,000, tickets price are:

`p(18,000)=-0.0006*18,000 +21.6\\p = \$10.80`