Question

A 49.0 kg wheel, essentially a thin hoop with radius 0.730 m, is rotating at 114 rev/min. It must be brought to a stop in 22.0 s. (a) How much work must be done to stop it? (b) What is the required average power? Give absolute values for both parts.

Answer 1

Step-by-step explanation:

Mass of the wheel, m = 49 kg

Radius of the hoop, r = 0.73 m

Initial angular speed of the wheel,
`\omega_i=114\ rev/min = 11.93\ rad/s`

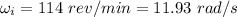
Final angular speed of the wheel,
`\omega_f=0`

Time, t = 22 s

(a) If I is the moment of inertia of the hoop. It is equal to,

`I=mr^2`

`I=49* (0.73)^2`

`I=26.11\ kg-m^2`

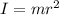
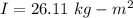
We know that the work done is equal to change in kinetic energy.

`W=\Delta E`

`W=(1)/(2)I(\omega_f^2-\omega_i^2)`

`W=-(1)/(2)* 26.11* (11.93^2)`

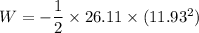
W = -1858.05 Joules

(b) Let P is the average power. It is given by :

`P=(W)/(t)`

`P=(1858.05\ J)/(22\ s)`

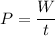
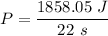
P =84.45 watts

Hence, this is the required solution.