Question

The numerator of a fraction is 1 less than the denominator if 4 is added to both the numerator and denominator the fraction becomes 8/4 find the fraction

Answer 1

The fraction is
`(6)/(5)`

Solution:

Let the denominator of fraction be "a"

Given that numerator of a fraction is 1 less than the denominator

numerator of a fraction = denominator - 1

So the numerator of a fraction = a - 1

Thus the required fraction is:

`\frac{\text {numerator}}{\text {denominator}}=(a-1)/(a)`

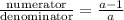
Also given that if 4 is added to both the numerator and denominator the fraction becomes 8/4

`\begin{array}{l}{\frac{\text {numerator}+4}{\text {denominator}+4}=(a-1+4)/(a+4)=(8)/(4)} \\\\ {(a-1+4)/(a+4)=(8)/(4)} \\\\ {(a+3)/(a+4)=2} \\\\ {a+3=2(a+4)} \\\\ {a+3=2 a+8} \\\\ {a=-5}\end{array}`

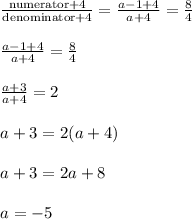
Thus the original fraction is:

`\frac{\text {numerator}}{\text {denominator}}=(a-1)/(a)=(-5-1)/(-5)=(-6)/(-5)=(6)/(5)`

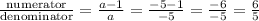
Thus the fraction is
`(6)/(5)`